Trójkąty :
Wielokątem o najmniejszej liczbie boków jest trójkąt, czyli płaszczyzna ograniczona najmniejszą liczbą linii prostych.
Trójkąt pitagorejski
Trójkąt pitagorejski to trójkąt prostokątny, którego długości boków są wyrażone liczbami naturalnymi.
Przykłady trójkątów pitagorejskich: (3,4,5), (5,12,13), (7,24,25).
Trójkąt Egipski
Trójkąt o bokach 3, 4, 5 to jedyny trójkąt prostokątny, którego długości boków są kolejnymi liczbami naturalnymi. Nazywa się go trójkątem egipskim, ponieważ był używany przez Egipcjan do wyznaczania kąta prostego w terenie.
Trójkąt Pascala
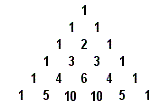 Trójkąt Pascala to trójkątna tablica, której pierwszy wiersz stanowi liczba 1, a każdy następny powstaje w ten sposób, że pod każdymi dwoma sąsiednimi wyrazami poprzedniego wiersza wpisuje się ich sumę, a na początku i na końcu każdego nowego wiersza dopisuje się jedynki.
Trójkąt Pascala to trójkątna tablica, której pierwszy wiersz stanowi liczba 1, a każdy następny powstaje w ten sposób, że pod każdymi dwoma sąsiednimi wyrazami poprzedniego wiersza wpisuje się ich sumę, a na początku i na końcu każdego nowego wiersza dopisuje się jedynki.
Liczby widniejące w n+1 wierszu trójkąta są współczynnikami rozwinięcia n-tej potęgi dwumianu. W czwartym wierszu, na przykład, stoją: 1, 3, 3, 1, a trzecia potęga, czyli sześcian dwumianu, dany jest wzorem:
(a+b)3 = a3 + 3a2b + 3ab2 + b3
Trókąt Pascala jest ściśle związany z symbolem Newtona.
Gwiazda pitagorejska :
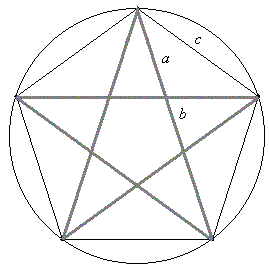
Umiłowaną figurą geometryczną pitagorejczyków był pentagram, zwany również gwiazdą pitagorejską. Jest to prawidłowy pięciokąt, którego boki przedłużone w obie strony tworzą pięciokąt gwiaździsty. Znakiem tym pitagorejczycy pozdrawiali się i wzajemnie rozpoznawali, kreśląc go na piasku.
Gwiazda pitagorejska posiada właściwości wyróżniające ją spośród innych gwiazd. Suma kątów wewnętrznych pentagramu równa jest kątowi półpełnemu (180°). Promienie gwiazdy pitagorejskiej "tworzą" trójkąty równoramienne z dwoma kątami u podstawy 72° i kątem przy wierzchołku równym 36°. Możemy doszukać się więć trójkątów podobnych, z kórych wynika, że długośc odcinka a + b równa jest długości odcinka c.
Odcinek a + b jest przykładem złotej proporcji, czyli taki podział odcinka na dwie części, że większa część do mniejszej ma się tak samo jak całość do części wększej. Takie złote cięcia odnajdujemy we wszystkich punktach skrzyżowania promieni gwiazdy pitagorejskiej.
Pierwsze liczydła :
W starożytności naturalnym sposobem pomagania sobie w obliczeniach było odkładanie kamieni, a sposobem zapisu karbowanie kresek na kiju. Najstarszym powszechnie używanym przyrządem służącym do liczenia było liczydło (abakus). Nazwa pochodzi od greckiego abax, co oznacza płytę, prawdopodobnie dlatego, ze niegdyś kamyki umieszczano w wyrytych żłobkach płytki albo w ziemi.

Liczydła miały wiele zróżnicowanych form. Najczęściej były to prostokątne deski z wyżłobionymi rowkami, w których ułożone kamyki oznaczają poszczególne pozycje przedstawianej cyfry. Dodając i odejmując kamienie w rzędach wykonywało się operacje arytmetyczne.
Najstarszym znanym mechanicznym urządzeniem liczącym był mechanizm odnaleziony we wraku statku koło wyspy Antikythera. Jego odnalezienie, a właściwie rekonstrukcja wykonana na podstawie zdjęć rentgenowskich wywołało sensację ponieważ brak jest pisanych źródeł na temat podobnych urządzeń w tamtych czasach. Skonstruowany prawdopodobnie na Rodos około 87 roku n.e. składał się z 37 kół zębatych wykonanych z brązu umieszczonych w drewnianej ramie. Przypuszcza się, że służył do obliczeń astronomicznych.
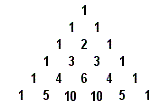 Trójkąt Pascala to trójkątna tablica, której pierwszy wiersz stanowi liczba 1, a każdy następny powstaje w ten sposób, że pod każdymi dwoma sąsiednimi wyrazami poprzedniego wiersza wpisuje się ich sumę, a na początku i na końcu każdego nowego wiersza dopisuje się jedynki.
Trójkąt Pascala to trójkątna tablica, której pierwszy wiersz stanowi liczba 1, a każdy następny powstaje w ten sposób, że pod każdymi dwoma sąsiednimi wyrazami poprzedniego wiersza wpisuje się ich sumę, a na początku i na końcu każdego nowego wiersza dopisuje się jedynki. 